1以上N以下の3つの整数の和

ABC-200のE問題"Patisserie ABC 2"が時間中にACできなくて悔しすぎるので勢いで書きます。

問題中、 ${(i,j,k)\in \lbrack 1,N\rbrack}^3$ での ${i+j+k=a}$ の解の個数と、 ${(j,k)\in \lbrack 1,N\rbrack}^2$ での ${j+k=b}$ の解の個数を考える箇所があります。

後者に関しては以下のように図形的に解釈して適当に場合分けすれば ${b}$ に対する閉じた式が得られるでしょう。結構別の場面でも見る気がします。それに比べると前者はやや複雑です。

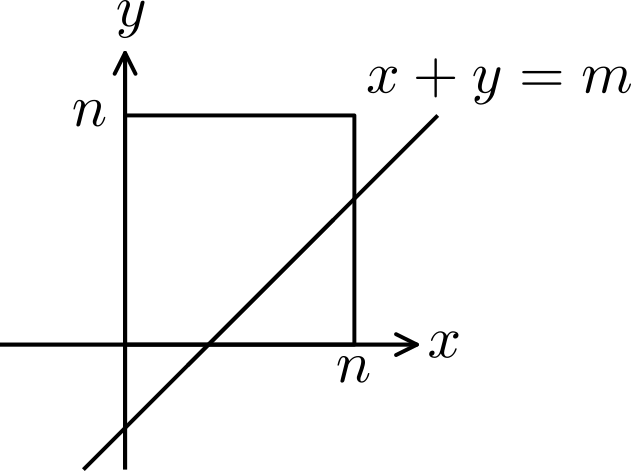
f:id:rotsuka691:20210508234751p:plain — 図形的イメージ

両方とも母函数を考えれば簡単です。
\begin{align}
\left(x+x^2+\cdots+x^N\right)^3 &= x^3 \left( \frac{1-x^N}{1-x} \right)^3\\
&= x^3\sum_{k=0}^\infty \binom{k+2}{2} x^k \left(1-3x^N+3x^{2N}-x^{3N} \right)
\end{align}
から、 ${i+j+k=a=a'+3}$ の解の個数は、
\begin{align}
\delta(a'\geq 0)\binom{a'+2}{2} - 3\delta(a'\geq N)\binom{a'-N+2}{2} + 3\delta(a'\geq 2N)\binom{a'-2N+2}{2} - \delta(a'\geq 3N) \binom{a'-3N+2}{2} .
\end{align}
ただし
\begin{align}
\delta(P) =
\left\{\begin{array}{cc}
1&\mbox{if}\, P\,\mbox{is true,}\\
0&\mbox{otherwise}
\end{array}\right.
\end{align}
（要は真偽値の01への暗黙の変換の関数的表現）です。

（ ${a'}$ の区間で場合分けした形にも書き直せますが）正負を問わず全ての整数 ${a'}$ で同じ見た目の式が成立するというのが肝です。

同様に、 ${j+k=b=b'+2}$ の解の個数は、
\begin{align}
\delta(b'\geq 0)\binom{b'+1}{1} - 2\delta(b'\geq N)\binom{b'-N+1}{1} + \delta(b'\geq 2N)\binom{b'-2N+1}{1}
\end{align}
と書けます。この表現なら場合分けでの事故が防げそうですね。（まあ関数化すれば済む話ですが）