1以上N以下の3つの整数の和
ABC-200のE問題"Patisserie ABC 2"が時間中にACできなくて悔しすぎるので勢いで書きます。
問題中、 での
の解の個数と、
での
の解の個数を考える箇所があります。
後者に関しては以下のように図形的に解釈して適当に場合分けすれば に対する閉じた式が得られるでしょう。結構別の場面でも見る気がします。それに比べると前者はやや複雑です。
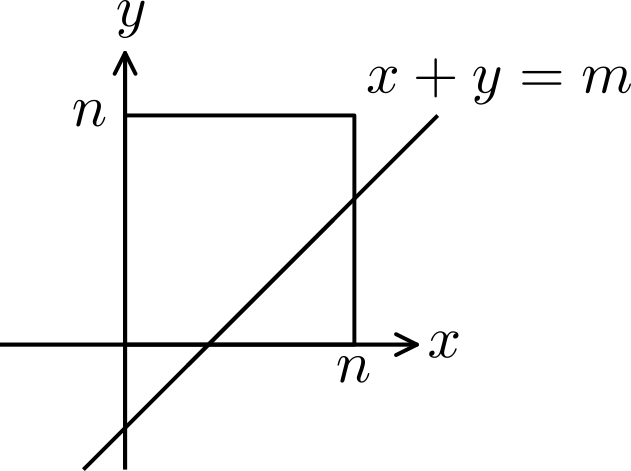
両方とも母函数を考えれば簡単です。
\begin{align}
\left(x+x^2+\cdots+x^N\right)^3 &= x^3 \left( \frac{1-x^N}{1-x} \right)^3\\
&= x^3\sum_{k=0}^\infty \binom{k+2}{2} x^k \left(1-3x^N+3x^{2N}-x^{3N} \right)
\end{align}
から、 の解の個数は、
\begin{align}
\delta(a'\geq 0)\binom{a'+2}{2} - 3\delta(a'\geq N)\binom{a'-N+2}{2} + 3\delta(a'\geq 2N)\binom{a'-2N+2}{2} - \delta(a'\geq 3N) \binom{a'-3N+2}{2} .
\end{align}
ただし
\begin{align}
\delta(P) =
\left\{\begin{array}{cc}
1&\mbox{if}\, P\,\mbox{is true,}\\
0&\mbox{otherwise}
\end{array}\right.
\end{align}
(要は真偽値の01への暗黙の変換の関数的表現)です。
(の区間で場合分けした形にも書き直せますが)正負を問わず全ての整数
で同じ見た目の式が成立するというのが肝です。
同様に、 の解の個数は、
\begin{align}
\delta(b'\geq 0)\binom{b'+1}{1} - 2\delta(b'\geq N)\binom{b'-N+1}{1} + \delta(b'\geq 2N)\binom{b'-2N+1}{1}
\end{align}
と書けます。この表現なら場合分けでの事故が防げそうですね。(まあ関数化すれば済む話ですが)
あーーーーーーー悔しい………………………………
これを考えた経験があれば時間内にデバッグできたかもしれない……………………
教訓:
- 「何番目」は1引く。配列のインデックスと同様。
- 区間
も ずらして
で考える。
- カウンタ変数とlong longとの演算がある場合には、repマクロは使わず明示的にfor文を書いた方がいいかも?
- 「区間に含まれているか否か」を考える場合は基本的に半開区間
で考える。
追記
OEISを見に行く方法もあるようです。
A109439 - OEIS
"Triangle read by rows, in which row n gives coefficients in expansion of ( (1 - x^n)/(1 - x) )^3."
ABC198F-Cubeを群論と母関数で解く
ABC198F-Cubeは、群論と母関数の知識を活かすことができるという意味で典型的な組合せ論の問題です。
結論から書くと、入力 に対して
として、答えは
をで割った余りです。ただし、
は床関数、
は
を
で割った余り、
とします。
C++による解答例:
atcoder.jp
公式の解説にも引用されているOEISのA054473にあるように、の母関数は
です。これを示したのち、上に掲げた の閉じた表式
を導出してみましょう。
固定点を数える
立方体の回転について
立方体(正六面体)を自分自身に移すような回転(向きを変えない=反転を含まない)の全体は、位数24の正六面体群 をなします。この群は立方体の各面の中心を結んでできる正八面体に対して同時に作用するため、しばしば正八面体群と呼ばれます。
立方体の4本の対角線 に注目すると、回転と同時にこれらに対して置換として作用していることが分かります。実は立方体の回転によって対角線たちを移し合う全ての置換が可能で、逆にある置換はただ一つの立方体の回転に対応します。すなわち、正六面体群
は4次対称群
と同型です。このことを知っていると、あとで回転を列挙するときに見通しが良くなります。
Cauchy-Frobeniusの補題
群論の言葉を使って問題を言い換えましょう。元の問題では和が の正の整数を各面に書くことになっていますが、全ての面から1を引いて和が
の非負整数を書くことを考えても同じことなので、以後これを考えることにします。
一般に、集合 に対して有限群
が作用するとき、軌道(
の作用による
の同値類)の個数は
の各元の不動点の個数の平均になります。これを Burnsideの補題、あるいは Cauchy-Frobeniusの補題 と呼びます。
Burnside's lemma - Wikipedia
Orbit-counting theorem - Groupprops
群の各元に対して不動点を数えるのは、軌道の代表元を漏れなく列挙することに比べれば容易です。実際には全ての元を調べる必要すらなく、共役類の代表元に対して数え上げれば十分です。これは、群のふたつの元が同じ共役類に属していれば、作用する有限集合に引き起こす置換の型が一致するためです(逆は成り立ちません)。
は下の図に示す特定の割り当てかたを考えることにします。

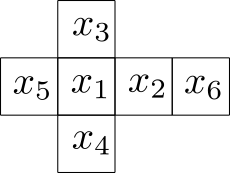
立方体の回転に応じて各変数がどのように移り合うか調べていきます。
不動点を数える
正六面体群 のある元
に対して、
の作用による
の不動点の集合を
で表すことにします。Cauchy-Frobeniusの定理から、
正六面体群 は、回転の様子に対応して以下に挙げる5つの共役類(順に
とします)に分割されます;
向かい合う面の中心を結ぶ直線に関する1/2回転: 共役類A
このような回転は向かい合う面のペアのそれぞれに対してひとつ存在するため、合わせて3つです。
上下の面 以外は向かい合う面に移り合います。置換のサイクル表記では
です。このとき対角線に対しては
という置換が引き起こされています。
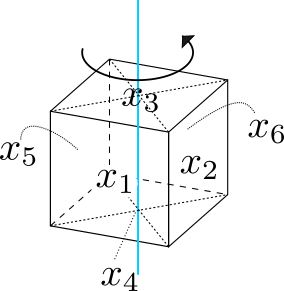
この作用に対する不動点であるためには かつ
であることが必要十分です。したがって、
以下同じ要領で調べられるため、概要のみ書くことにします。
対角線に関する1/3回転: 共役類B
このような回転は4本の各対角線に対して右/左ねじどちらに回すかに応じて存在するため、合わせて8つです。
面に書かれた数の置換:
対角線の置換:

向かい合う辺の中点を結ぶ直線に関する1/2回転: 共役類C
このような回転は向かい合う辺のペアごとに存在するため、合わせて6つです。
面に書かれた数の置換:
対角線の置換:
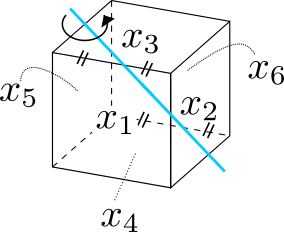
向かい合う面の中心を結ぶ直線に関する1/4回転: 共役類D
回転軸は と同じで、回転角だけが異なります。このような回転は各面に対して右ねじの向きでひとつずつ存在するため、合わせて6つです。
面に書かれた数の置換:
対角線の置換:
以上の観察を表にまとめます。
母関数を展開する
共役類 に対して、
の母関数を
とします。
が分かります。ここにCauchy-Frobeniusの補題を利用すると、所望の の母関数は
と定まります。こうしてひとつにまとまりましたが、展開するにあたっては共役類ごとに見ていくと簡単です。
共役類Eに対する母関数
を展開するのはやさしいです。これは重複組合せの母関数です。
共役類B,Cに対する母関数
これもほぼ重複組合せの母関数ですが、の冪のみが異なります。
おまけ1
上の表から見て取れるように、各共役類は面の置換の型によって6の分割に対応します。ここでは6の分割11通りのうち5つが登場しましたが、残りの6つも示しておきましょう。
1+1+1+1+2
1+1+1+3
1+2+3
1+5
2+4
6
おまけ2
今回の問題に比べると、Wikipediaの記事にも例示されている立方体の面の塗分けの問題は母関数を考えなくてよいぶんかなり簡単です。最大 色で塗り分けるとすると、この中から置換のサイクルごとに色を取ればよいので、
A047780 - OEIS "Number of inequivalent ways to color faces of a cube using at most n colors."
まだ取り組んでいませんが、正(四|六|八|十二|二十)面体の(辺|面|頂点)で同様のことを考えると計算の練習になりそうです。